LSTM 是 1997 年的工作,而 GRU 是 2014 年基于 LSTM 精简改进而来的。
我们会先介绍 GRU.
GRU#
使用门(Gate)来控制隐藏层的更新。
具体来说,是两个门:Reset Gate,Update Gate
这些“门”,都是直接基于 每一时刻的输入 Xt 和 上一时刻的隐藏层状态 ht−1 计算得来,并通过 sigmoid 得到各元素介于 0 和 1 之间的向量,称为门的状态向量。将门的状态向量与经过门的向量进行逐元素乘法“⊙”,得到门的输出。
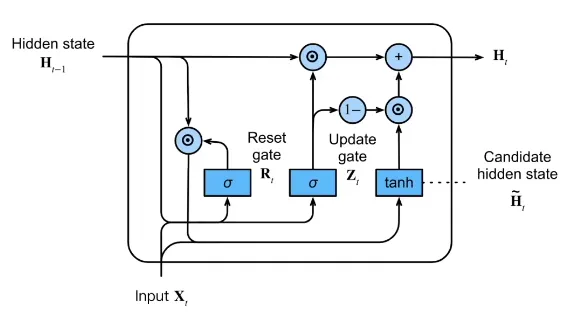
Reset Gate, Rt#
门的状态公式:
Rt=σ(XtWxr+ht−1Whr+br)
Reset Gate 控制的是「候选的新隐藏层状态 h~t」有多少取决于上一时刻的隐藏层状态 ht−1,即:
h~t=tanh(XtWxh+(Rt⊙ht−1)Whh+bh)
Update Gate, Zt#
门的状态公式:
Zt=σ(XtWxz+ht−1Whz+bz)
Update Gate 控制的是「新的隐藏层状态 ht」中,上一时刻隐藏层状态 ht−1 和 候选的新隐藏层状态 h~t 的比例,即:
ht=Zt⊙ht−1+(1−Zt)⊙h~t
Zt=1 时,完全延续旧的 ht−1;
Zt=0 时,完全使用候选的新隐藏层状态 h~t,而抛弃旧的隐藏层状态。
不难看出,GRU 的两个门并不是完全正交的,而是存在耦合。当 Zt=1 的时候,无论 Rt 如何取值,结果都相同,即完全延续旧的 ht−1. 此时 Update Gate 的作用覆盖了 Reset Gate.
但这种耦合被证明对模型训练是有促进作用的,将这两个门改成更加解耦的尝试大多导致稳定性、表达能力、训练复杂度的劣化。
设想一下,假如去除了 Reset Gate,那么有两种处理方式:
- 每次计算 h~t 的时候,输入中的 Xt 和 ht−1 各占一半(或某种固定的比例),那么模型就永远无法产生一个与 ht−1 无关的 ht,限制了模型调整状态、适应突变输出的能力。
- 每次计算 h~t 的时候,只参考 Xt,然后通过 Zt 混合新旧隐藏层状态。这样的问题也很明显,新旧记忆只能做逐元素的线性混合,抑制了模型的推理能力。
由此可知,Reset Gate 并不是多余的。
LSTM#
应该理解为 Long Short-Term Memory,即长的短期记忆网络,而不存在什么“长期记忆”。
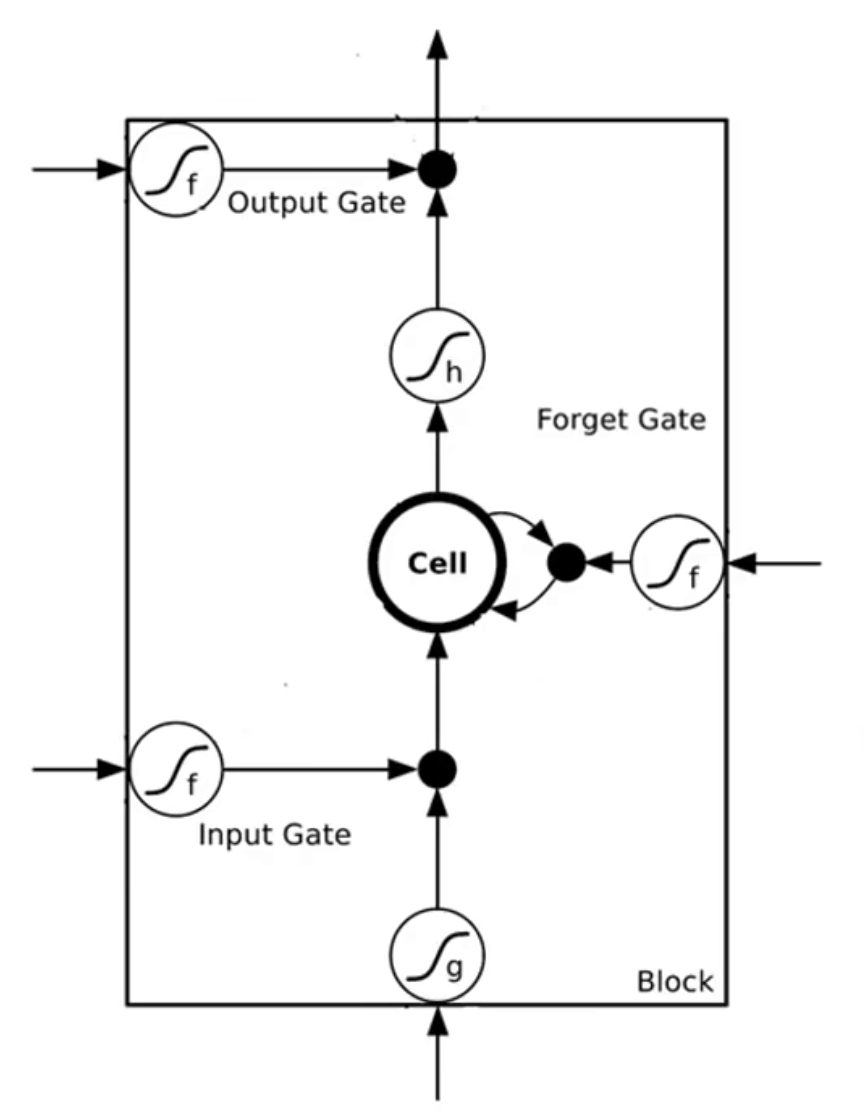
李宏毅老师的简化版 LSTM 结构图
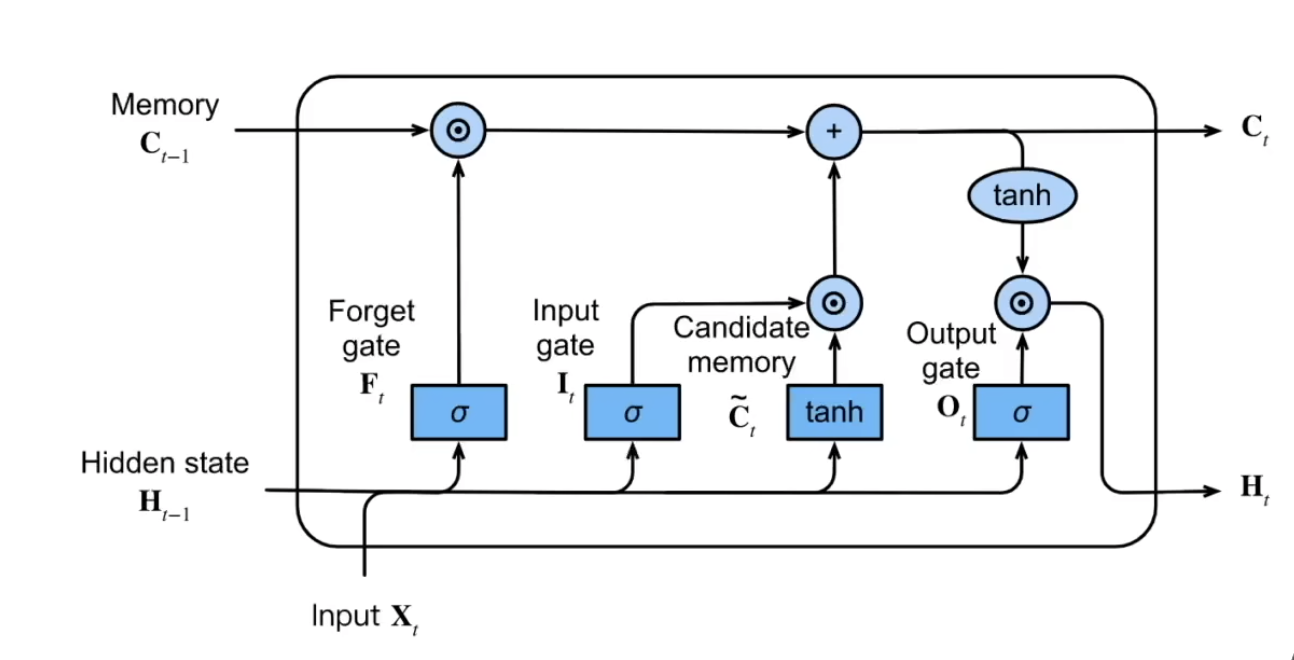
李沐老师的完整 LSTM 结构图
LSTM 同样使用门,但它的结构更加清晰,各个门的分工更加明确,可解释性更强。
LSTM 将 Hidden State 作为很短的短期记忆以及每次对外输出的接口,而 Memory Cell 则专门存储较长的记忆。
这一点与 GRU 区别明显:GRU 的记忆全部混在 Hidden State 中,输出就是记忆。
它使用三个门 Input Gate,Forget Gate,Output Gate 来控制记忆的流动。
产生候选新记忆 C~t#
C~t 的产生不经过任何门的控制,总是会考虑当前的输入和之前的记忆(因此不如 GRU 灵活),公式为:
C~t=tanh(XtWxc+ht−1Whc+bc)
门的状态公式:
It=σ(XtWxi+ht−1Whi+bi)
Input Gate 控制的是「产生的候选新记忆 C~t」 进入新记忆 Ct 的权重。
Forget Gate, Ft#
门的状态公式:
Ft=σ(XtWxf+ht−1Whf+bf)
Forget Gate 控制的是「旧的记忆 Ct−1」有多少能延续到新的记忆 Ct 中,因此也许叫作保留门而不是遗忘门更好。
Input Gate 和 Forget Gate 合起来的作用是:
Ct=Ft⊙Ct−1+It⊙C~t
Output Gate, Ot#
门的状态公式:
Ot=σ(XtWxo+ht−1Who+bo)
Output Gate 控制的是记忆 Ct 流出到新的隐藏层状态 ht 的量,即:
ht=Ot⊙tanh(Ct)
LSTM 的输出的唯一来源是记忆(没有从上一时刻的 Hidden State 直接到这一时刻的输出的通路),而记忆则是由旧记忆和新记忆混合而成的。
与 GPT 的 Q & A#
为什么要多次使用 tanh?#
LSTM 在产生新记忆、输出记忆到隐藏层的时候均使用了 tanh(相当于压缩到值域 (−1,1)),但是 Cell State Ct 本身没有被压缩过,这里面有特殊的考量:
- C~t 必须用 tanh——为了限制新增记忆的“写入幅度”
- Ct 不用 tanh——为了让信息可以线性累积、不被压缩,因此 Ct 可能比较大
- 输出 ht 要用 tanh——为了把 Ct 的可能大值映射回可控范围
如果这里对 Cell State 再套一个 tanh,就会导致
- 信息很快被 squash 到 [−1,1]
- 长期记忆会丢失(不断 tanh,会持续压缩)
✦ LSTM 最重要的发明就是通过这条几乎线性的路径
让梯度可以沿着 Cell State 回传,而不被消耗掉。
如果你对 Cell State 使用 tanh:
- 梯度会持续被 tanh′<1 的导数衰减
- 记忆和梯度都会消失(失去 LSTM 的价值)
所以:
Cell State 是不应该加 tanh 的,因为 LSTM 想保留一条“无激活函数”的梯度高速公路。
为什么要同时传递 Cell State 和 Hidden State?#
✅ 结论先说:只有 Cell State 是不够的。必须有 Hidden State,原因包括以下核心点:
- Cell State 本质上只负责“长期记忆”,它不经过 tanh,不适合直接在每个时刻表达高维抽象特征
- 门控需要一个“压缩版”的状态参与计算,而不能直接用 Cell State
- 理论上,LSTM 设计来自于为了解决梯度消失:Cell State 保留线性路径,而 Cell State 保留非线性路径
- 如果只传递 Cell State,本质上你就变成了一个“简化版 LSTM”,跟 GRU 很接近,但会损失表达能力
| 功能 | c_t(cell) | h_t(hidden) |
|---|
| 长期记忆 | ✔ | ✘ |
| 梯度高速公路 | ✔ | ✘ |
| 非线性激活表达(短期) | ✘(不能加,否则破坏梯度) | ✔ |
| 门控输入的摘要 | ✘(不适合直接暴露) | ✔ |
| 输出到下一层 | ✘(线性记忆不适合输出) | ✔ |
深层 RNN#
每一层的输出(即 Hidden State)同时作为当前时刻的下一层的输入,和本层下一时刻的输入。
双向 RNN#
将 RNN 网络的每一层都加倍一份,给第一份输入正向序列,给第二份输入倒着的序列,再把其输出倒转回来,和第一份的输出直接 concat 拼接在一起,然后一起输入到下一层。这样,双向 RNN 除了最下面的一层,每一层的输入尺寸都会扩大到 2 × num_hiddens,但是每层正反向的输出大小仍然是 num_hiddens,因此能保持层间 features 维度不会无限扩大。最后输入 FC 层(此时的 FC 层的输入特征数量加倍了)进行预测和训练。
这里的“倒转”是从时间(也就是 num_steps)的角度而言。
双向 RNN 可以做文本分类、机器翻译、语音识别、完形填空,但是单纯的预测未来(比如序列生成)十分不靠谱!


