PyTorch 自动微分与反向传播 • CoderXL's Blog

理论支持#

链式法则#

求导原理告诉我们，每一种运算都对应着导数上的一种运算。
例如： $(u+v)' = u' + v'$ ， $(u(v))'=u'(v)v'$ ……
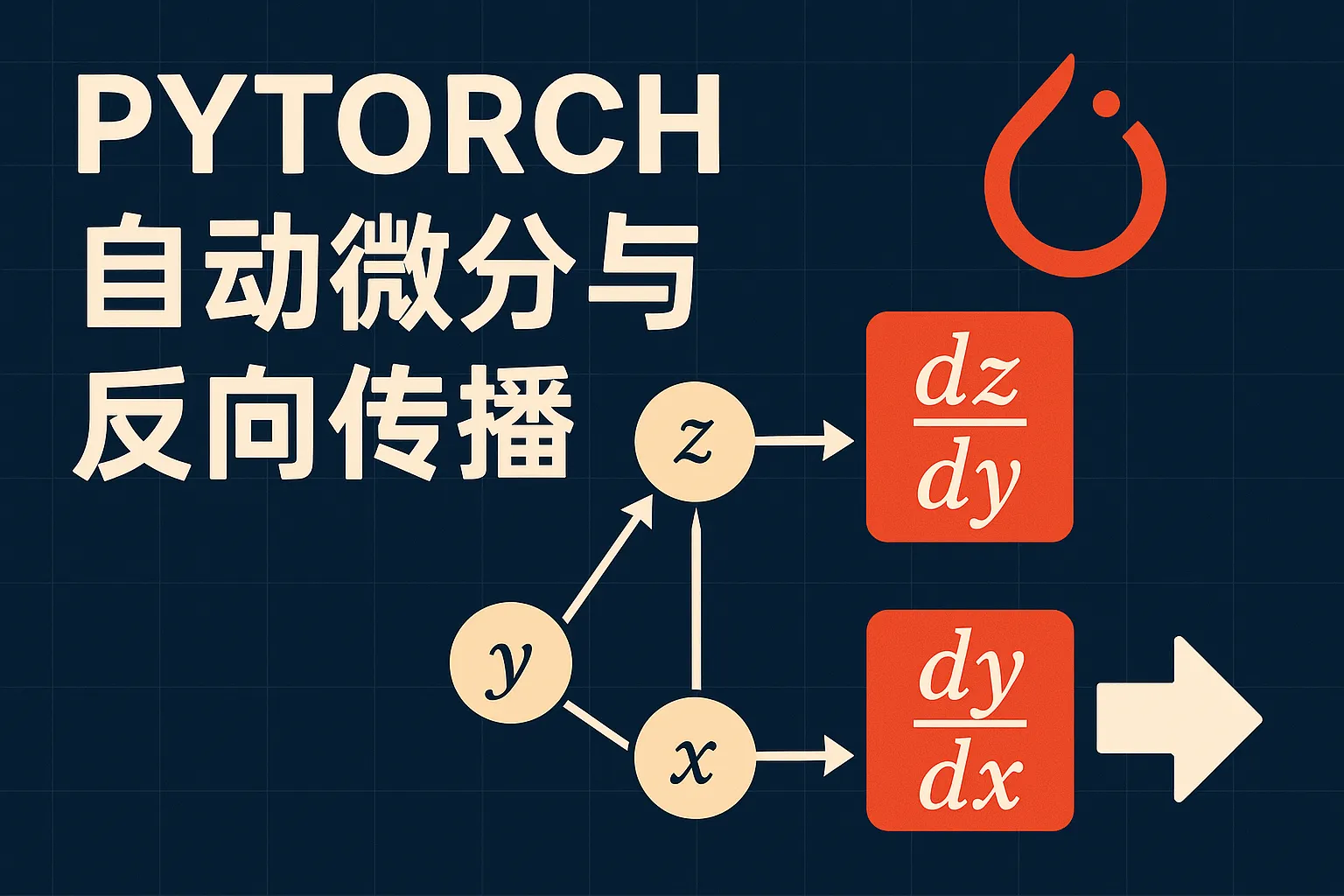
因此，可以构建一个有向无环的“计算图”，它的起点们（入度为零）是各个自变量，终点（出度为零）是一个因变量，中间节点是各种运算符（运算符其实等同于中间变量，因为运算符与其结果一一对应，故而之后不再区分计算图中的运算符和变量）。
注意，计算图是 DAG 而不是树，因为同一个变量可以被多个变量引用，而多个变量也可以被同一个变量引用。

构建好之后，我们的计算图应当长这样：具有一个终点（因变量）和至少一个起点（自变量）。只有这样，才能应用经典的反向传播算法。事实上，深度学习中需要梯度下降的情况基本都是大量输入（参数、数据）对应一个输出（损失函数值），因此这个条件比较容易被满足。

然后，开始反向传播。在计算图上，从因变量（设为 $y$ ）开始，对每个相连的上游变量 $u_i$ ，计算 $\displaystyle{\partial y\over \partial u_i}$ ，然后 BFS 到上游一层，继续对每个中间变量的上游变量 $v_{i,j}$ 计算 $\displaystyle{\partial u_i \over \partial v_{i,j}}$ ，并与之前累计的导数相乘……最后，到达每个自变量。
根据全微分公式，某个变量的全微分一定是它对各个上游变量的偏导的线性组合：

\mathrm{d} f=\frac{\partial f}{\partial x} \mathrm{~d} x+\frac{\partial f}{\partial y} \mathrm{~d} y+\frac{\partial f}{\partial t} \mathrm{~d} t .

因此，如果有多个路径抵达了同一个自变量，那么因变量对该自变量的偏导一定是把各个路径的微分结果直接加和得到。

实现原理#

反向传播使用的是“精确的”数值求导。既不是 SymPy 的符号运算（精确），也不是有限差分的 $\varepsilon$ 近似（数值）。而是对一个特定的输入输出值，在计算图上逐步应用链式法则。所以节点之间传递的是梯度数值（而不是符号化的公式），最终也只能得到该输入输出情况下的梯度数值，而得不到一个通用的梯度公式。这样做的好处是既保留了精确求导的精度，有节约了符号求导的时间。代价是对于不同的输入输出，每次都需要重新 forward 计算因变量，再 backward 计算梯度。

实际例子：#

y=x^3+x^2

flowchart LR
	subgraph B["反向传播"]
		Y2["$$y=u+v$$"]
		Y2 --> |"$${\partial y \over \partial u}=1$$"| U2["$$u=x^3$$"]
		Y2 --> |"$${\partial y \over \partial v}=1$$"| V2["$$v=x^2$$"]
		X2["$$x$$"]
		U2 --> |"$$({\partial y \over \partial u}){\partial u \over \partial x}=3x^2$$"| X2
		V2 --> |"$$({\partial y \over \partial v}){\partial v \over \partial x}=2x$$"| X2
	end
	subgraph A["计算图"]
		Y["$$y=x^3+x^2$$"]
		Y --> U["$$u=x^3$$"]
		Y --> V["$$v=x^2$$"]
		X["$$x$$"]
		U --> X
		V --> X
	end

对于 $\displaystyle{\mathrm{d} y \over \mathrm{d} x}$ ，只需要将到达 $x$ 的多条路径直接相加即可： $\displaystyle{{\mathrm{d} y \over \mathrm{d} x} = 3x^2 + 2x}$

另一个例子：#

y={\sin x \over x}

flowchart LR
	subgraph B["反向传播"]
		Y2["$$y={u\over x}$$"]
		X2["$$x$$"]
		Y2 --> |"$${\partial y \over \partial u}={1\over x}$$"| U2["$$u=\sin x$$"]
		Y2 --> |"$${\partial y \over \partial x}=-{u \over x^2}$$"| X2
		U2 --> |"$$({\partial y \over \partial u}){\partial u \over \partial x}={\cos x \over x}$$"| X2
	end
	subgraph A["计算图"]
		Y["$$y={\sin x \over x}$$"]
		X["$$x$$"]
		Y --> U["$$u=\sin x$$"]
		Y --> X
		U --> X
	end

同样，只需要直接相加： $\displaystyle{{\mathrm{d} y \over \mathrm{d} x} = {\cos x \over x} - {\sin x \over x^2}}$

可恶，Mermaid 不可以画反向的箭头，害得我计算图也只能从上到下了。。。

代码细节#

PyTorch 和 TensorFlow 2.x 采用隐式构建计算图（Dynamic Graph / Eager Execution），类似于一些软件的“宏录制”功能。在声明了需要记录某个变量的计算过程后，就可以在正常的运算中，边计算实际结果，边记录运算过程来构建计算图。实际原理包括重载运算符魔法函数（比如 __add__ __mul__）。
隐式构建可以较为容易地修改、拼接现有代码和第三方代码，还方便调试。

相比之下，TensorFlow 1.x 就需要显式构建计算图（Static Graph），即先构建，后计算。需要先定义占位符，书写表达式，最后使用 tf.Session() 统一计算，计算要手动 feed 和 fetch，十分繁琐。

import torch

x = torch.arange(4, dtype=torch.float32)    # tensor([0., 1., 2., 3.])

# 声明需要记录计算图。作用是给 x attach 一个 grad 属性，以存储未来算好的梯度
# 等价于定义变量时传入 requires_grad=True
x.requires_grad_(True)    # tensor([0., 1., 2., 3.], requires_grad=True)

# 计算 y
y = 2 * torch.dot(x, x)    # tensor(28., grad_fn=<MulBackward0>)

# 通过计算图推导 y 对 x 的偏导
# 从 y 推到 x
y.backward()

print(x.grad)    # tensor([ 0.,  4.,  8., 12.])
print(x.grad == 4 * x)    # tensor([True, True, True, True])

根据理论支持中提出的原理，反向传播应该由因变量发起，并且计算完成后，因变量对各个自变量（requires_grad==True 的那些）的梯度都会由相应自变量存储在自己的 .grad 属性中。

不难看出，计算图里的每个节点在 BFS 的时候都需要临时存储 .grad，因此反向传播对内存消耗比较大。